More from the lovely Grandma Luce:
Ah Grandma Luce, it appears that it is your goodself that is somewhat lacking in mathematical technique, shall we have a look why?
You say that the Autodynamics Velocity sum equation is:
Bn = (1 - ( (1- B1^2) ...... (1- (Bn-1)^2)))^1/2
Which indeed it is, as the page I linked to clearly demonstrates, however in my large post I was asking the question what happens to the AD velocity sum equation at low velocities, where C >> V? (In this case as long as v is less than about 10% of C this approximation holds very well)
Well what happens is that your equation above reduces to:
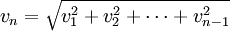(I believe from a technical standpoint that you use a Taylor expansion to get to this from the AD equation.)
Exactly as I had stated. For fun, and because I do this kind of thing everyday I decided using IDL to check that this is the case (hey nothing better to do), If I use the equation given by Grandma Luce and values of v1=10000., v2=20000. and v3=30000. we get a velocity total of 374165.67, if we use the equation above we get 374165.74. Proving again that it is an excellent low velocity limit for the equation given by Grandma Luce.
Oh and also that AD is a crock. Its nice to see one of the ADiots admit that the velocity sum does apply in cases of relative motion though, and hence the world can now see that it is clearly contradicted by the real world, I mean if you throw a ball in the direction of motion at 10m/s from a train travelling at 10m/s, what does someone stationary on the ground see? The ball travelling at 20m/s (as in the real world) or 14.14m/s as in the AD fantasy land? You decide.
On a final note to Grandma Luce, if you don't mind would you enlighten us as to what your PhD is in? Oh and thanks for playing! Try again soon!
Dear Mark:
You are very very ignorant.
The equation that I sent to you is exactly the same as PAGE reference. What really happen, is that you don't know Elemental Algebra, neither the order on how the operations are made.
Ignorant like you cannot study Physics. Change your career. You are making the ridiculous-man
As always, thanks for your Propaganda
Regards.
Lucy Haye.
Ah Grandma Luce, it appears that it is your goodself that is somewhat lacking in mathematical technique, shall we have a look why?
You say that the Autodynamics Velocity sum equation is:
Bn = (1 - ( (1- B1^2) ...... (1- (Bn-1)^2)))^1/2
Which indeed it is, as the page I linked to clearly demonstrates, however in my large post I was asking the question what happens to the AD velocity sum equation at low velocities, where C >> V? (In this case as long as v is less than about 10% of C this approximation holds very well)
Well what happens is that your equation above reduces to:
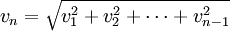(I believe from a technical standpoint that you use a Taylor expansion to get to this from the AD equation.)Exactly as I had stated. For fun, and because I do this kind of thing everyday I decided using IDL to check that this is the case (hey nothing better to do), If I use the equation given by Grandma Luce and values of v1=10000., v2=20000. and v3=30000. we get a velocity total of 374165.67, if we use the equation above we get 374165.74. Proving again that it is an excellent low velocity limit for the equation given by Grandma Luce.
Oh and also that AD is a crock. Its nice to see one of the ADiots admit that the velocity sum does apply in cases of relative motion though, and hence the world can now see that it is clearly contradicted by the real world, I mean if you throw a ball in the direction of motion at 10m/s from a train travelling at 10m/s, what does someone stationary on the ground see? The ball travelling at 20m/s (as in the real world) or 14.14m/s as in the AD fantasy land? You decide.
On a final note to Grandma Luce, if you don't mind would you enlighten us as to what your PhD is in? Oh and thanks for playing! Try again soon!
No comments:
Post a Comment